

Startseite - Zurück - Vorwärts
 |
1. Ableitung von Geraden
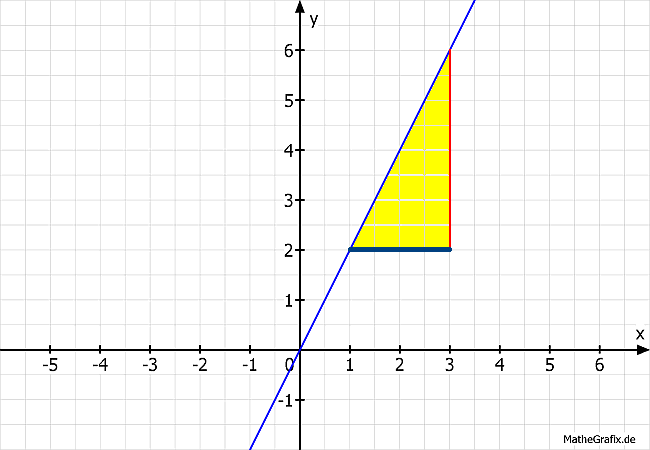
1. Beispiel: Wir betrachten die Funktion f(x) = 2 x Sie hat immer und an jedem Punkt die Steigung 2. Stellen Sie sich vor, sie gehen diese Gerade hinauf, und zwar immer von links nach rechts. Wenn Sie zum Beispiel sich auf der x-Achse 10 m nach rechts bewegen, dann haben Sie auf der y-Achse 20 m an Höhe gewonnen. Die Steigung einer Geraden ist immer gleich. Am Steigungsdreieck können sie unmittelbar die Steigung der Geraden ablesen: Steigung = Die Länge der senkrechten Seite geteilt durch die Länge der waagrechten Seite. Im Bespiel ist die Steigung also 4 geteilt durch 2 = 2. Ganz einfach. Nun kommt die Ableitung ins Spiel, um die Steigung zu ermitteln. Wenn f(x) = 2 x dann ist die Ableitung davon f´(x) = 2 Die Ableitung beschreibt also für jeden Punkt der Funktion die Steigung. Da die Steigung einer Geraden für jeden Punkt gleich ist, erhalten wir als Ableitung eine Gerade, die parallel zu x-Achse verläuft, also waagrecht ist. 2. Beispiel. Wir haben die Gerade f(x) = 0,5x = x / 2 = (1 / 2) * x, welche zur Verdeutlichung mit verschiedenen Schreibweisen dargestellt ist. Dann ist die Ableitung davon f´(x) = 0,5 = 1 / 2 Allgemein können wir für die Ableitung von Geraden schreiben: f(x) = a * x f´(x) = a Das x wird einfach wegestrichen. So einfach werden Geraden abgeleitet. Das ist der ganze Witz beim Ableiten mit Geraden. Diese Animation zeigt , was passiert, wenn a verändert wird. Die blauen Geraden sind die Ableitungen der roten Grafen. Dies gilt auch, wenn a eine negative Zahl ist: Ein Beispiel: f(x) = - 3x Stellen Sie sich vor, Sie gehen auf dem Grafen von links nach rechts. Dann geht es bergab. Die Ableitung lautet f´(x) = -3 und bildet eine Gerade, weil es immer mit dem gleichen Gefälle bergab geht. Es handelt sich also umgangssprachlich nicht um eine Steigung, sondern um ein Gefälle. Eine negative Steigung ist immer ein Gefälle. Deshalb lautet die Ableitung f´(x) = -3 Sonderfälle: Und nun kommen die Sonderfälle, die sich ebenalls alle (bis auf eine Ausnahme) mit der bekannten Regel f(x) = a * x f´(x) = a plausibel erklären lassen. Sonderfälle werden immer gerne in Prüfungen und Klassenarbeiten getestet, um zu sehen, ob jemand abstrakt denken kann: 1. Sonderfall: a = 0 f(x) = 0 * x = 0 f´(x) = 0 Auch hier wurde einfach das x weggestrichen. 2. Sonderfall: a = 1 f(x) = 1 * x = x f´(x) = 1 Jetzt können Sie als f(x) = x ableiten. Auch hier wurde wieder das x entfernt. Diese Regel gilt dann auch entsprechend, wenn a = -1. 3. Sonderfall: a = - 1 f(x) = -1 * x = -x f´(x) = -1 Jetzt können sie also auch f(x) = -x ableiten und bekommen keine Panik beim Anblick des Minuszeichens. Erinnern Sie sich einfach, dass -x die andere Schreibweise für -1 * x ist. Dann brauchen sie nur das x entfernen. 4. Sonderfall: f(x) = a f(x) = a f´(x) = 0 Warum? Weil f(x) = a immer eine Parallele zur x-Achse darstellt. Stellen sich sich vor, sie gehen auf dieser Geraden entlang. Sie ist ebenerdig. Null Steigung, Null Gefälle. Deshalb ist die Ableitung 0. Addition und Subtraktion von Geraden: 1. Beispiel: f(x) = 3 x + 6 x - 2 x Wie lautet die Ableitung?. Wir müssen den Ausdruck auf der rechten Seite so umformen, dass nur ein x im Ausdruck steht: f(x) = 3 x + 6 x - 2 x f(x) = (3+6-2) * x f(x) = 7 x f´(x) = 7 Darauf wären Sie sicher selbst gekommen. Aber nun haben Sie die Bestätigung. 2. Beispiel: f(x) = 2 x + 3 f´(x) = 2 Warum? Der Summand 3 verschiebt den Graphen f(x) = 2 x nur um 3 nach oben. Die Steigung des Graphen ändert dadurch nicht. Stellen Sie sich vor, Sie besteigen einen Berg und die Steigung des Pfades beträgt 2. Es hat keinen Einfluss auf die Steigung, ob sich der Pfas 3 m oder 300 m über der Meereshöhe befindet. Entsprechend ist dann auch f(x) = 2 x - 3 f´(x) = 2 Division: 1. Fall: f(x) = 10 x / 5 x f(x) = 10 / 5; (das x kürzt sich raus) f(x) = 2 f´(x) = 0 2. Fall: f(x) = 8 x / 4 f(x) = (8/4) * x f(x) = 2 x f´(x) = 2 Einige Fälle, die im nächsten Kapitel behandelt werden: f(x) = 8 / x = 8 * x-1 f(x) = x2 Es geht also darum, wenn x einen Exponenten erhälten. Beachten Sie dabei auch, dass sich Wurzelausdrücke ebenfalls durch Exponenten ausdrücken lassen. Hier geht es weiter zum nächsten Kapitel. Doch vorher sollten sie mit Hilfe Übungsaufgaben die notwendige Routine und Sicherheit im Lösen der Aufgaben trainieren. Mathematik ist hauptsächlich Übungssache und weniger eine Frage der Intelligenz. |
Bis jetzt haben wir gelernt, wie mit Hilfe von Steigungdreiecken die Ableitung von Geraden gelingt. Das nachfolgende Video zeigt als Ausblick, wie mit Hilfe von Steigungdreiecken auf grafische Weise näherungsweise die Ableitung von nichtlinearen Funktionen gelingt:
Übungsaufgaben: Lösen Sie die
nachfolgenden
Aufgaben mit Papier und
Stift, damit Sie sich von Anfang an an die
Prüfungssituation
gewöhnen. Fortgeschrittene können auch versuchen die
Aufgaben im Kopf zu lösen. Das ist ein gutes Training. Die
Lösungen und Hinweise stehen im obigen Feld.
Versuchen Sie
erst selbst auf die Lösung zu kommen. Wenn Sie nicht
weiterwissen,
bekommen Sie Hilfestellungen, in dem Sie mit der Maus auf
"Lösungsansatz" fahren.
Wenn Sie auf "Ausführlicher Lösungsweg" klicken, erhalten Sie den vollständigen Lösungsweg als Spickzettel, dessen Fenster Sie aufzoomen können, um sich Schritt für Schritt die Lösung anzeigen lassen zu können, ohne das zu viel verraten wird.
| 1) f(x) = 2x - 3 + 4x | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |
| 2) f(x) = -2x - 5x - 3 | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |
| 3) f(x) = 6x - 6x - 6 | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |
| 4) f(x) = 4 * 5x - 8x / 4 - 6 | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |
| 5) f(x) = x | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |
| 6) f(x) = 0 | Lösung | Lösungsansatz | Ausführlicher Lösungsweg |